RUMUS BANGUN RUANG

Rumus-rumus Bangun Ruang

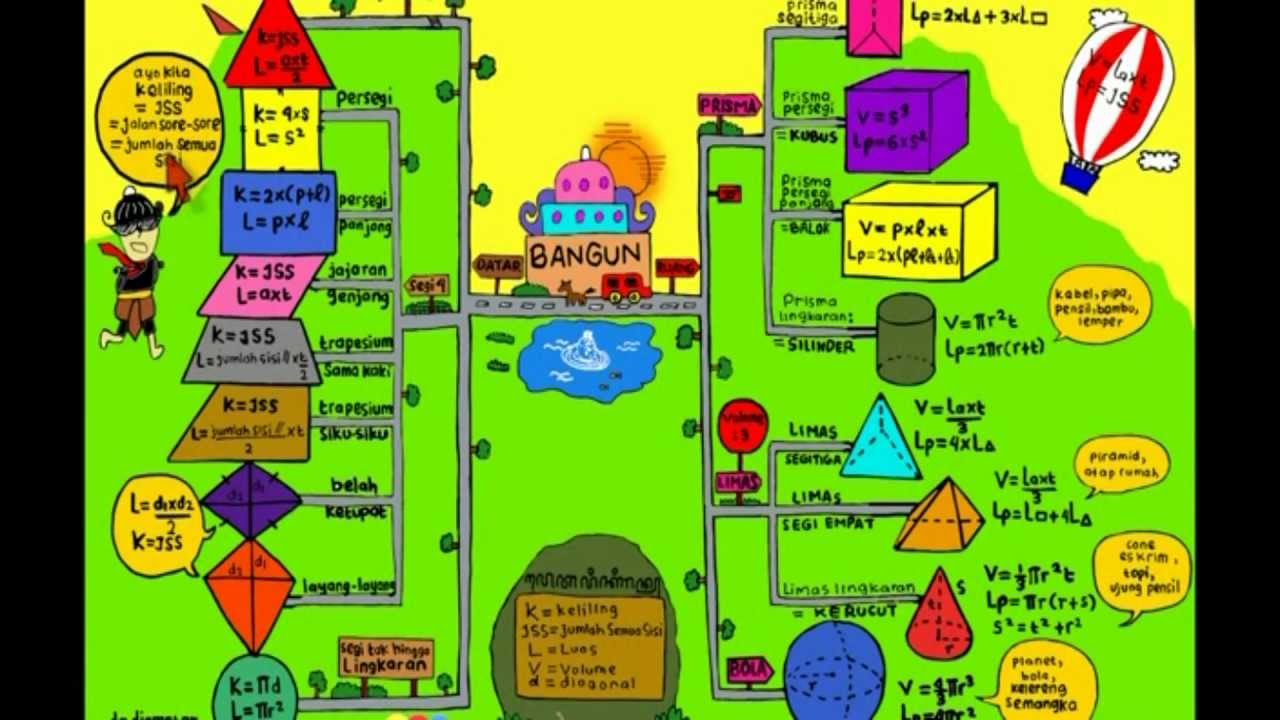ilmu matematika tidak pernah lepas dari rumus-rumus matematika mengenai bangun ruang seperti kubus, balok, kerucut, tabung, limas, dan bola. Artikel kali ini akan saya tuliskan tentang rumus bangun ruang yang ada di dalam pelajaran matematika seperti rumus kubus, rumus tabung, rumus limas, rumus kerucut,  untuk mengetahui / mempelajari / mengingat kembali luas dan volume masing-masing bangun ruang.

Bangun ruang berbeda dengan bangun datar didalam menentukan rumusnya , yaitu tergantung dari bentuk bangun masing-masing. Secara umum bentuk dari bangun ruang seperti kubus dkk adalah 3 dimensi yang mempunyai isi atau volume berbeda dengan bangun datar yang hanya 2 dimensi.

1. RUMUS BANGUN RUANG KUBUS

Kubus terdapat 6 (enam) buah sisi yang berbentuk persegi dengan luas yang sama besar diantara sisinya.
Terdapat 12 (dua belas) rusuk dengan panjang rusuk yang sama panjang.
Semua sudut bernilai 90 derajat ataupun siku-siku.


Rumus:

Luas salah satu sisi = rusuk x rusuk
Luas Permukaan Kubus = 6 x rusuk x rusuk
Keliling Kubus = 12 x rusuk
Volume Kubus = rusuk x rusuk x rusuk ( rusuk 3 )

 

2. RUMUS BANGUN RUANG BALOK

Rumus:

Luas Permukaan Balok = 2 x {(pxl) + (pxt) + (lxt)}
Diagonal Ruang = Akar dari (p kuadrat + l kuadrat + t kuadrat)
Keliling Balok = 4 x (p + l + t)
Volume Balok = p x l x t (sama dengan kubus, tapi semua rusuk kubus sama panjang).

3. RUMUS BANGUN RUANG BOLA 

Rumus:

Luas Bola = 4 x π x jari-jari x jari-jari, atau
                    4 x π x r2
Volume Bola = 4/3 x π x jari-jari x jari-jari x jari-jari
π  = 3,14 atau 22/7

 

4. RUMUS BANGUN RUANG TABUNG/SILINDER 

Rumus:


Volume = luas alas x tinggi, atau
                luas lingkaran x t
Luas = luas alas + luas tutup + luas selimut, atau
            ( 2 x π x r x r) + π x d x t)

5. RUMUS BANGUN RUANG KERUCUT 

Rumus:


Volume = 1/3 x π x r x r x t
Luas = luas alas + luas selimut

6. RUMUS BANGUN RUANG LIMAS

Rumus:

Volume = 1/3 luas alas tinggi sisi
Luas = luas alas + jumlah luas sisi tegak

Read more

Bilangan Bulat dan Operasi Matematikanya

Dear sobat, kali ini kita akan belajar salah satu jenis bilangan yaitu bilangan bulat berikut operasi bilangan tersebut. Selain bilangan bulat, perlu sobat ketahui masih ada jenis bilangan lain seperti bilangan real, bilangan rasional, bilangan irasional, bilangan pecahan, dan lain-lain. Jika sobat mengamati sebuah termometer yang memiliki satuan skala dari mulai angka yang kurang dari nol atau negatif sampai dengan skala angka yang lebih dari nol  atau angka postif, itulah sebagian dari yang kita namakan bilangan bulat.

Apa itu Bilangan Bulat?

Dari contoh termometer di atas, kita bisa mendefinisikan bilangan bulat sebagai kelompok bilangan yang memiliki karakteristik:

• terdiri dari bilangan-bilangan sebagai anggotanya
• semua bilangan yang merupakan anggotanya bisa bilangan positif atau negatif
• bilangan pecahan dan bilangan desimal tidak termasuk di dalamnya.

Berikut beberapa catatan dari bilangan bulat yang perlu sobat perhatikan:

• bilangan yang diikuti pecahan (bilangan pecahan campuran) atau bilangan yang diikuti koma dan desimal bukan merupakan bilangan bulat.
• nol adalah anggota bilangan bulat tidak seperti bilangan asli yang mulai dari angka 1,2,3, … dan seterusnya.
• sobat bisa mengatakan kalau bilangan bulat adalah gabungan bilangan negatif, nol, dan bilangan positif.
• untuk menuliskan suatu bilangan bulat sobat bisa menggunakan kurung {} seperti {…,-3,-2,-1,0,1,2,3,…} tanda …. menandakan bilangan bergerak sampai tak hingga.

Membaca dan Menulis Bilangan Bulat

Jika sebuah bilangan bulat itu positif sobat bisa membacanya hanya dengan menyebut nama bilangan tersebut atau bisa juga menambahkan menambahkan kata positif di depannya. Untuk penulisan bilangan bulat positif tidak perlu menambahkan tanda (+) kecuali pada bidang ilmu tertentu seperti kimia atau fisika untuk menyatakan muatan. 

Misalkan

Bilangan Bulat 2
Bisa dibaca : “dua” atau “positif dua”
Ditulis : 2

Jika bilangan bulat itu negatif maka harus dibaca dengan menyebutkan kata negatif sebelum nama bilangan itu dan penulisannya harus menggunakan tanda negatif, contoh

Bilangan Bulat -2
Dibaca : “negatif dua”
Ditulis : -2

Menetukan Letak Bilangan Bulat pada Garis Bilangan

Caranya sangat mudah. Bilangan bulat negatif negatif selalu disebelah kiri angka nol dimulai dari -1,-2,3,  dan terus ke kiri hingga – tak hingga. Bilangan bulat positif berada di sebelah kanan angka nol bergerak dari angak 1,2,3, dan seterusnya ke kanan sampai tak hingga.

Membandingkan Dua Buah Bilangan Bulat

Jika ada dua buah bilangan bulat -7 dan 2, manakah yang lebih besar? Utuk menentukan mana yang lebih besar dan mana yang lebih kecil sobat bisa menggunakan garis bilangan.

• semakin ke kanan maka bilangan akan semakin besar
• semakin ke kiri maka akan semakin kecil
• untuk bilanga negatif  -5 < -4, -2 < -1 dan setersunya

Contoh
Manakah yang lebih besar -450 atau -30? jawabannya adalah -30 karena jika diletakkan di garis bilangan letakknya di sebelah kanan -450.

Operasi Bilangan Bulat

Untuk operasi bilangan bulat, sobat bisa menggunakan diagram panah pada garis bilangan dengan ketentuan.

“Panjang diagaram menunjukkan jumlah satuan sedangkan arah panah menentukan positif atau negatif. Jika diagaram panah menuju ke arah kanan maka bilangan bulat positif, jika menuju ke arah kiri maka bilangan bulat negatif.”

Read more

PERKALIAN

Perkalian dengan pengali 11; 111; atau deretan angka 1 dan beberapa angka 9

A. Perkalian dengan pengali 11

       Perhatikan cara yang cepat dalam mencari hasil kalinya. Hitungan dimulai dari angka terakhir dan diakhiri dengan angka yang pertama. Demikian pula

Read more

Aplikasi penjawab soal matematika

Aplikasi penjawab soal matematika. Pasti dari kalian pernahkan yang namnya mengerjakan soal matematika. Bagaimana, susah atau sulit??

Nah di zaman yang semakin maju ini, semua pekerjaan manusia menjadi ringan dan sangat mudah untuk dikerjakan.
Tidak hanya dibidang ekonomi, perkembangan teknologi juga berkembang di dunia pendidikan, Salah satu buktinya adalah munculnya aplikasi android penjawab soal matematika.

Read more

Membuat Belajar Matematika Menjadi Bergairah

Membuat Belajar Matematika Menjadi Bergairah

Rasa takut terhadap pelajaran matematika (fobia matematika) sering kali menghinggapi perasaan para siswa dari tingkat SD sampai dengan SMA bahkan hingga perguruan tinggi. Padahal,

Read more

Cara cepat menghitung Lingkaran

Sebelumnya Mafia Online sudah memposting tentang hubungan sudut pusat  dengan panjang busur lingkaran dan cara mudah/cepat menghitung luas juring lingkaran.Postingan ini kembali membahas mengenai hubungan sudut pusat dengan panjang busur lingkaran, hanya saja cara penyelesaiannya lebih mudah dipahami sehingga pastinya dalam menjawab soal menjadi lebih cepat dari cara sebelumnya.

Read more

Hal yang Menyebabkan Matematika Membosankan

Penyebab Matematika Itu Membosankan

Matematika?????

 Siapa sih di sini yang seneng banget ama pelajaran Laknat yang satu itu.

Read more

AHLI MATEMATIKA TERKEMUKA DI DUNIA

10 AHLI MATEMATIKA TERKEMUKA DI DUNIA

1. Leonhard Euler

 

 Euler adalah ahli matematikayang hidup pada tahun 1707-1783, ia dianggap sebagai ahli matematika terhebat yang pernah berjalan di planet ini.

Read more

10 AHLI MATEMATIKA TERKEMUKA DI DUNIA

AHLI MATEMATIKA TERKEMUKA DI DUNIA

1. Leonhard Euler

 

 Euler adalah ahli matematikayang hidup pada tahun 1707-1783, ia dianggap sebagai ahli matematika terhebat yang pernah berjalan di planet ini.

Read more